🔢 1. Insertion Sort
Concept: Insertion Sort iteratively builds a sorted portion of the array, inserting each new element into its correct position within the sorted section.
Visual:

Python:
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr
Java:
public class InsertionSort {
public static void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}
}
C++:
void insertionSort(int arr[], int n) {
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}
JavaScript:
function insertionSort(arr) {
for (let i = 1; i < arr.length; i++) {
let key = arr[i];
let j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
return arr;
}
Complexity:
Time: O(n^2)
Space: O(1)
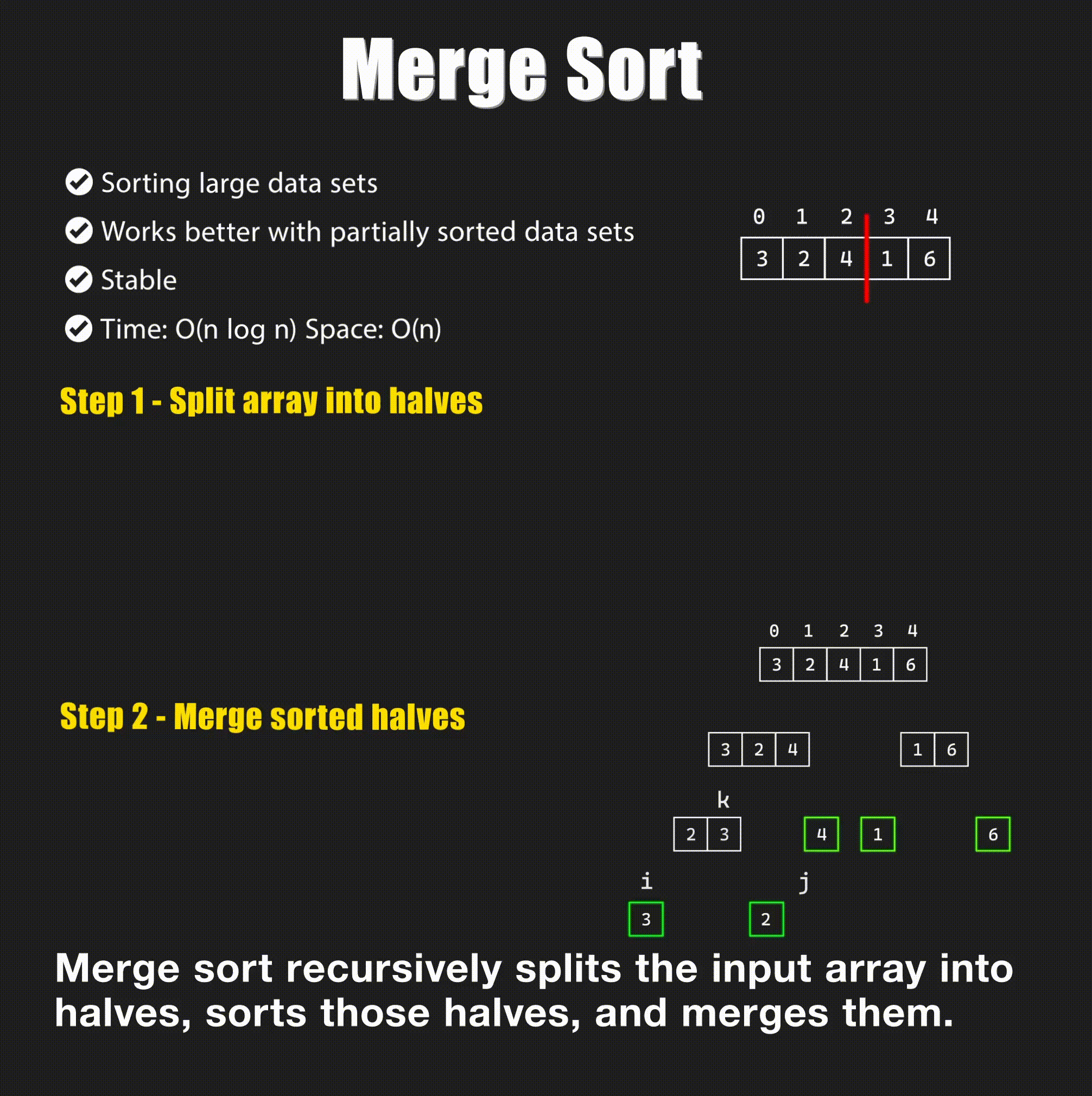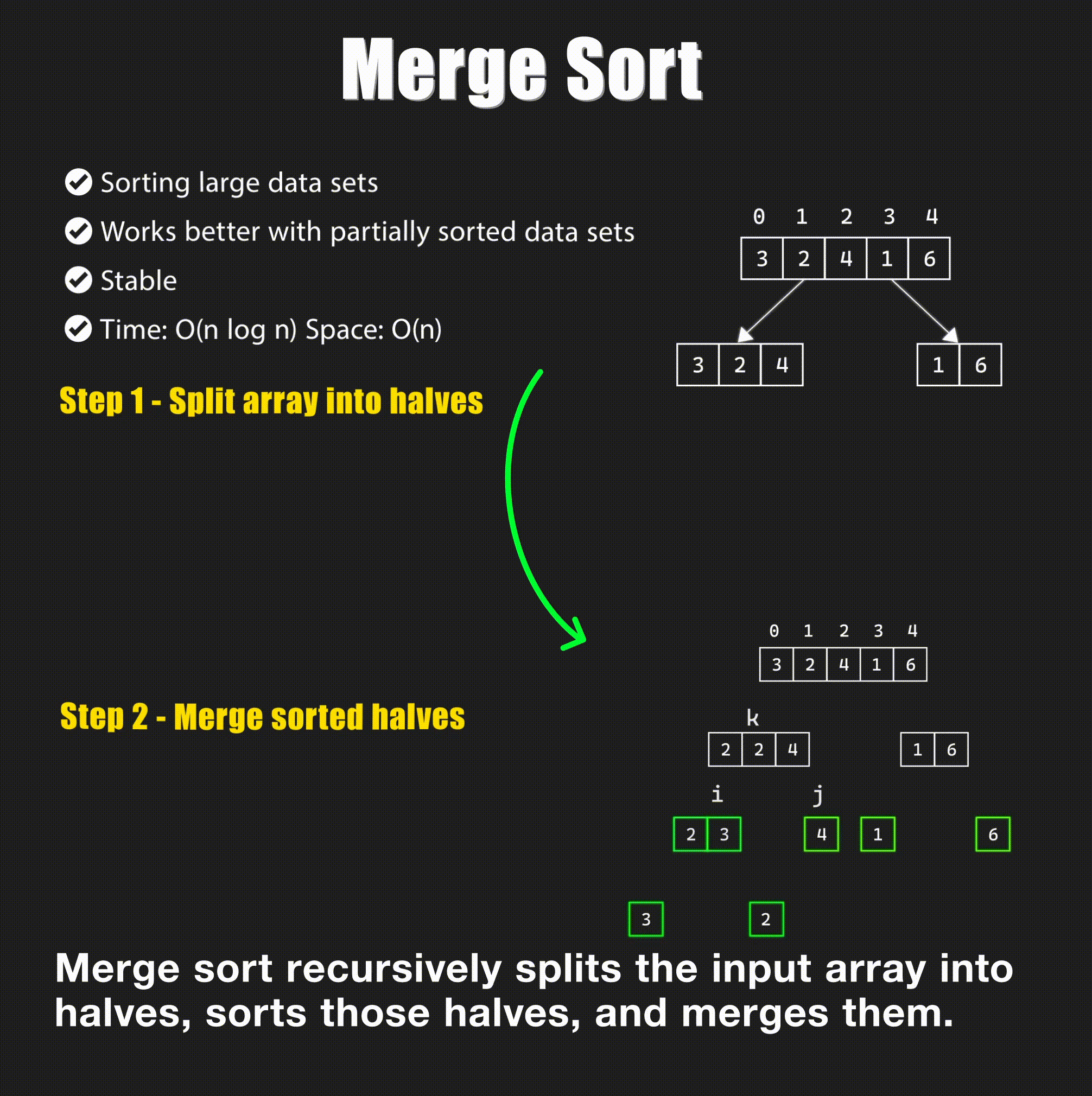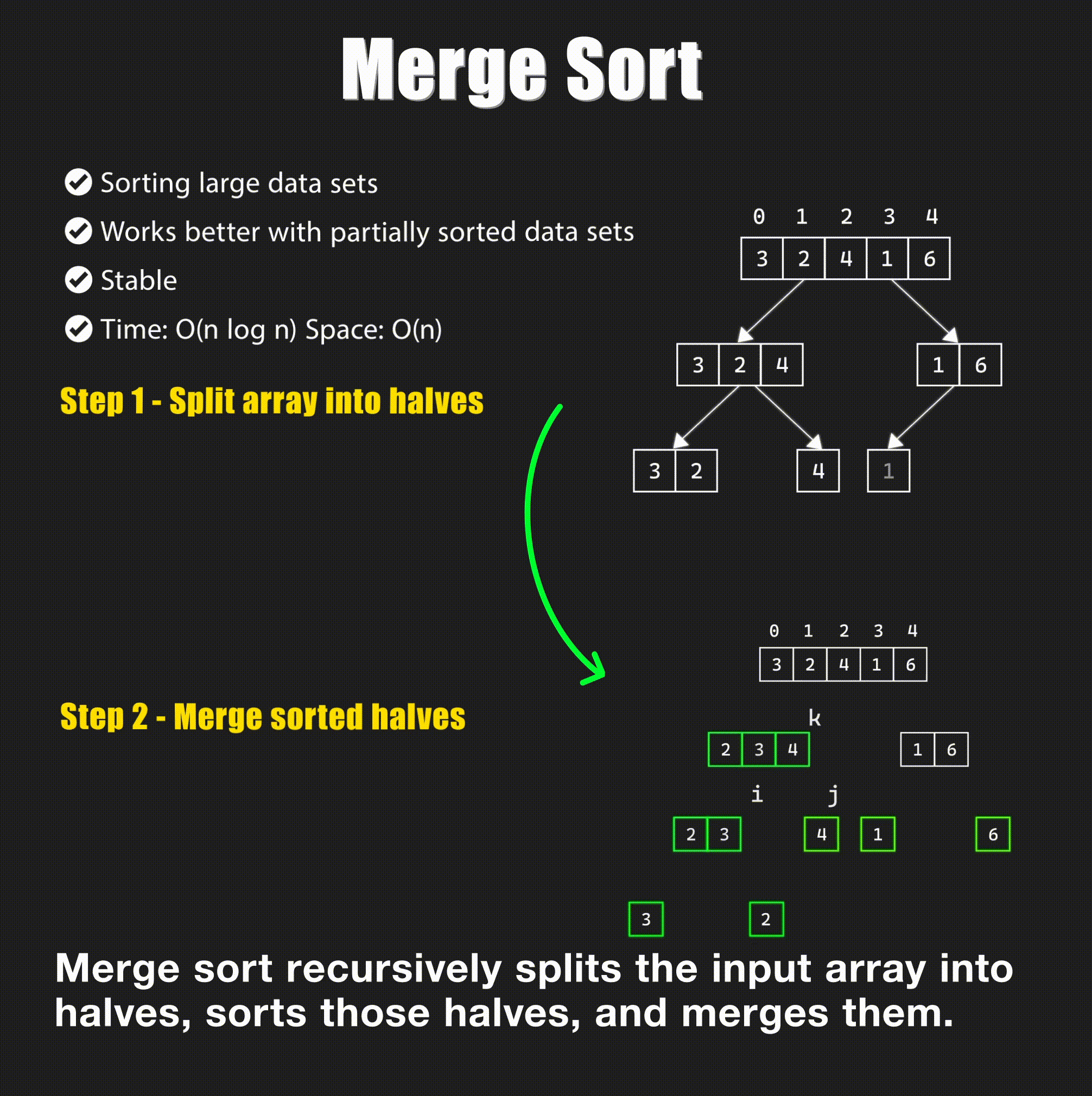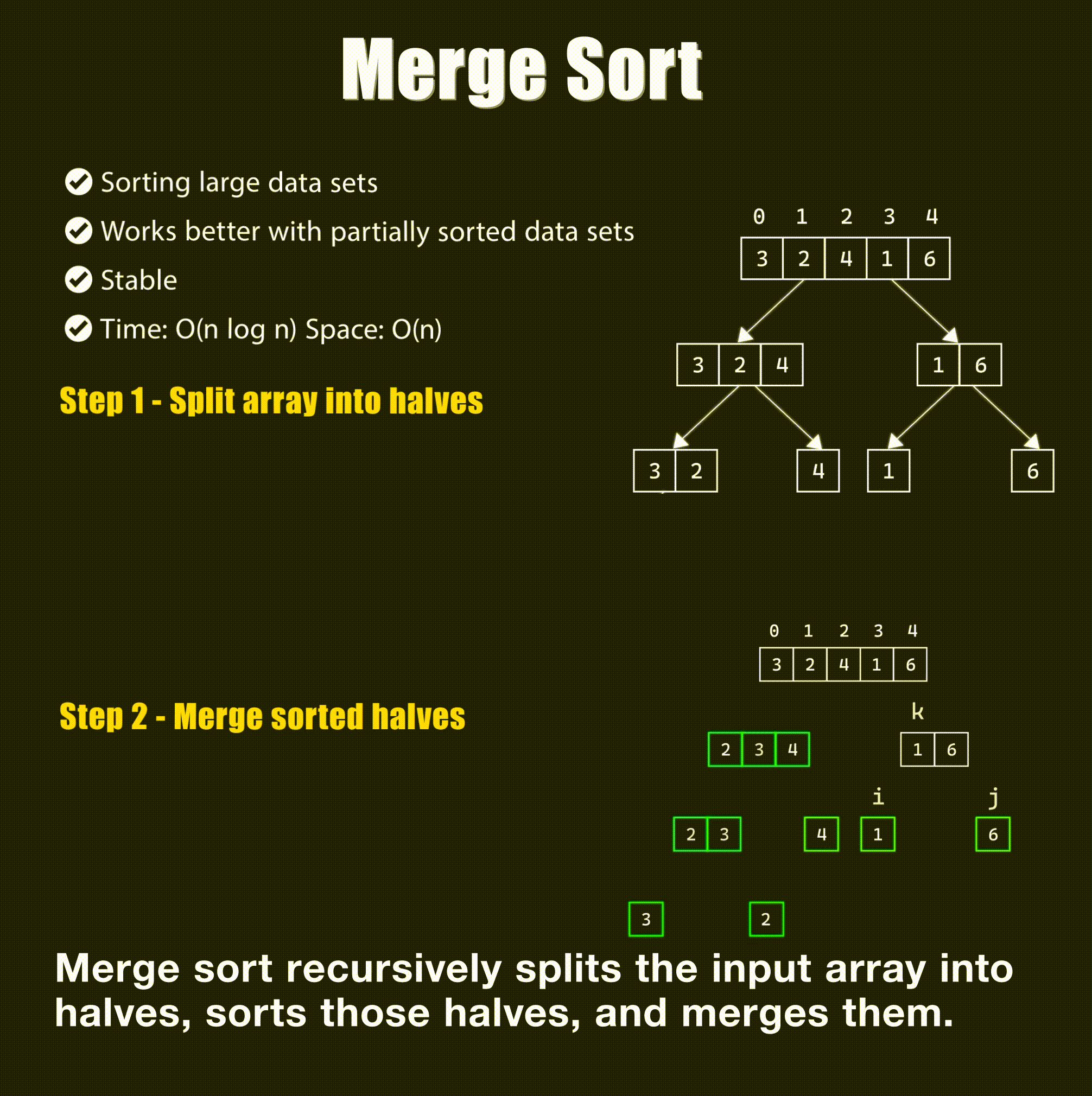
🔄 2. Merge Sort
Concept: Merge Sort splits the array into halves, recursively sorts them, and merges them back together.
Visual:
Python:
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
Java: (see original for full code) C++: (see original for full code) JavaScript: (see original for full code)
Complexity:
Time: O(n \log n)
Space: O(n)
🔄 3. Quick Sort
Concept: Quick Sort selects a pivot and partitions the array into elements less than and greater than the pivot.
Visual:

Python:
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
Complexity:
Time: O(n \log n) (average), O(n^2) (worst)
Space: O(\log n)
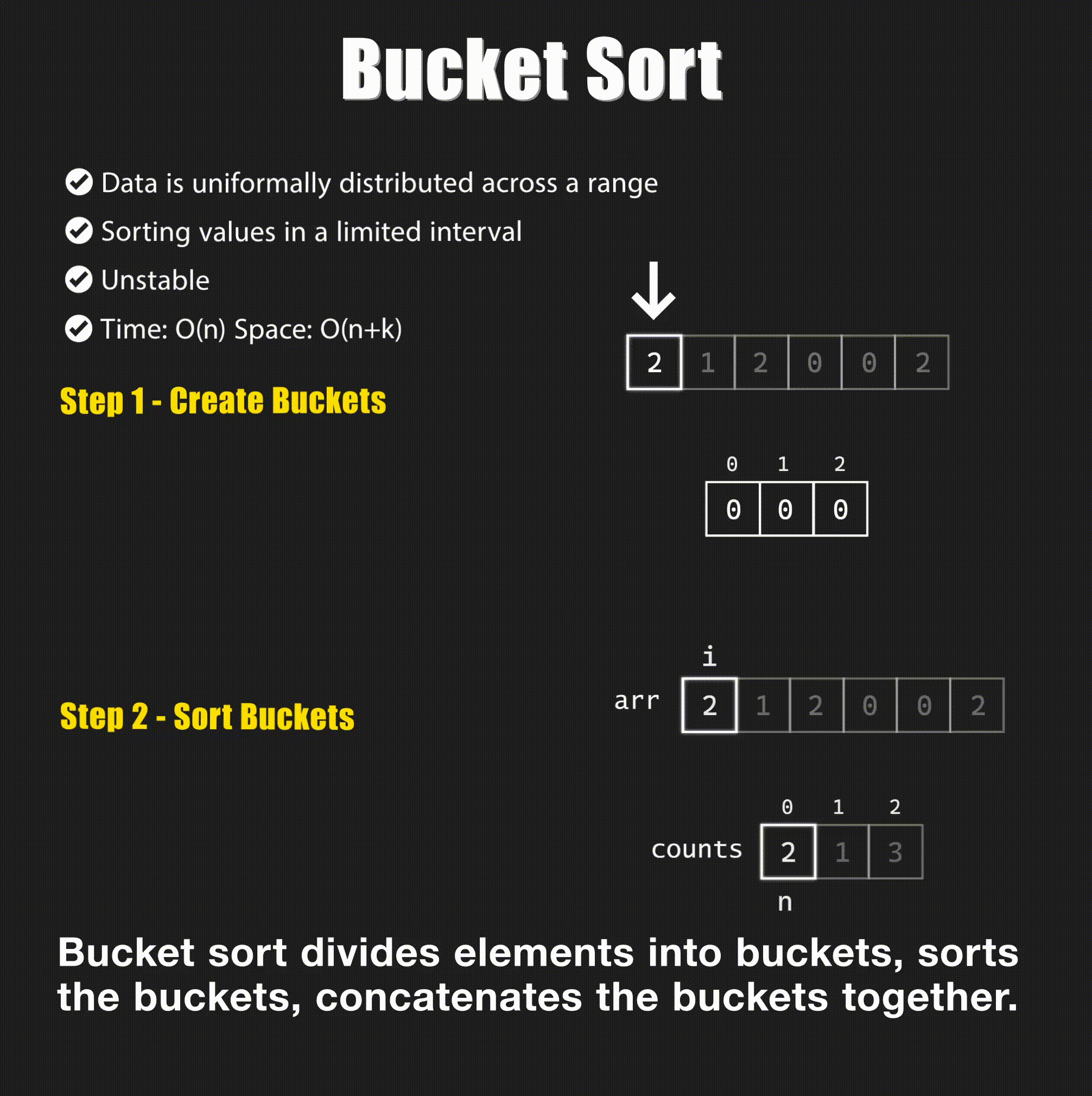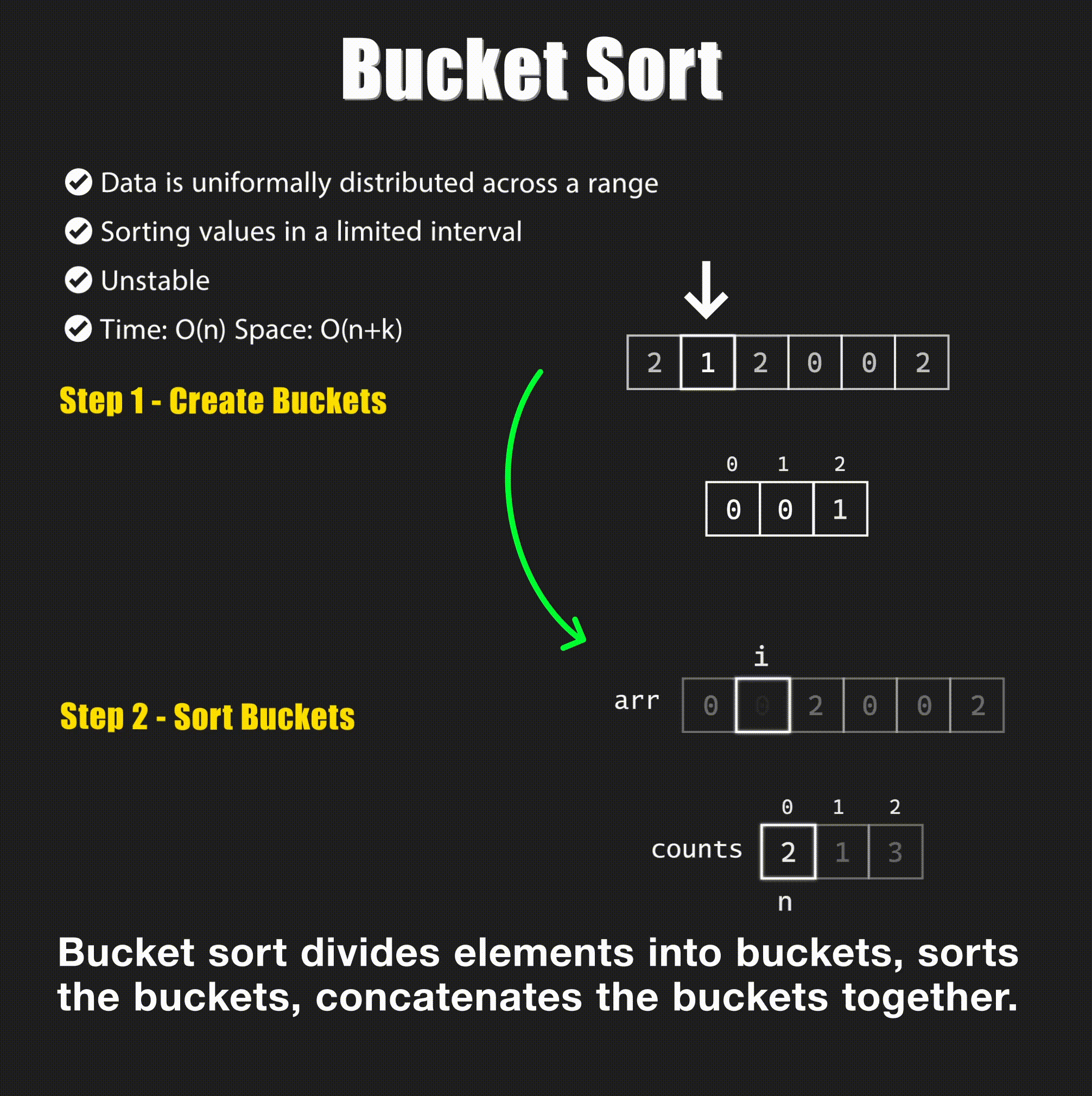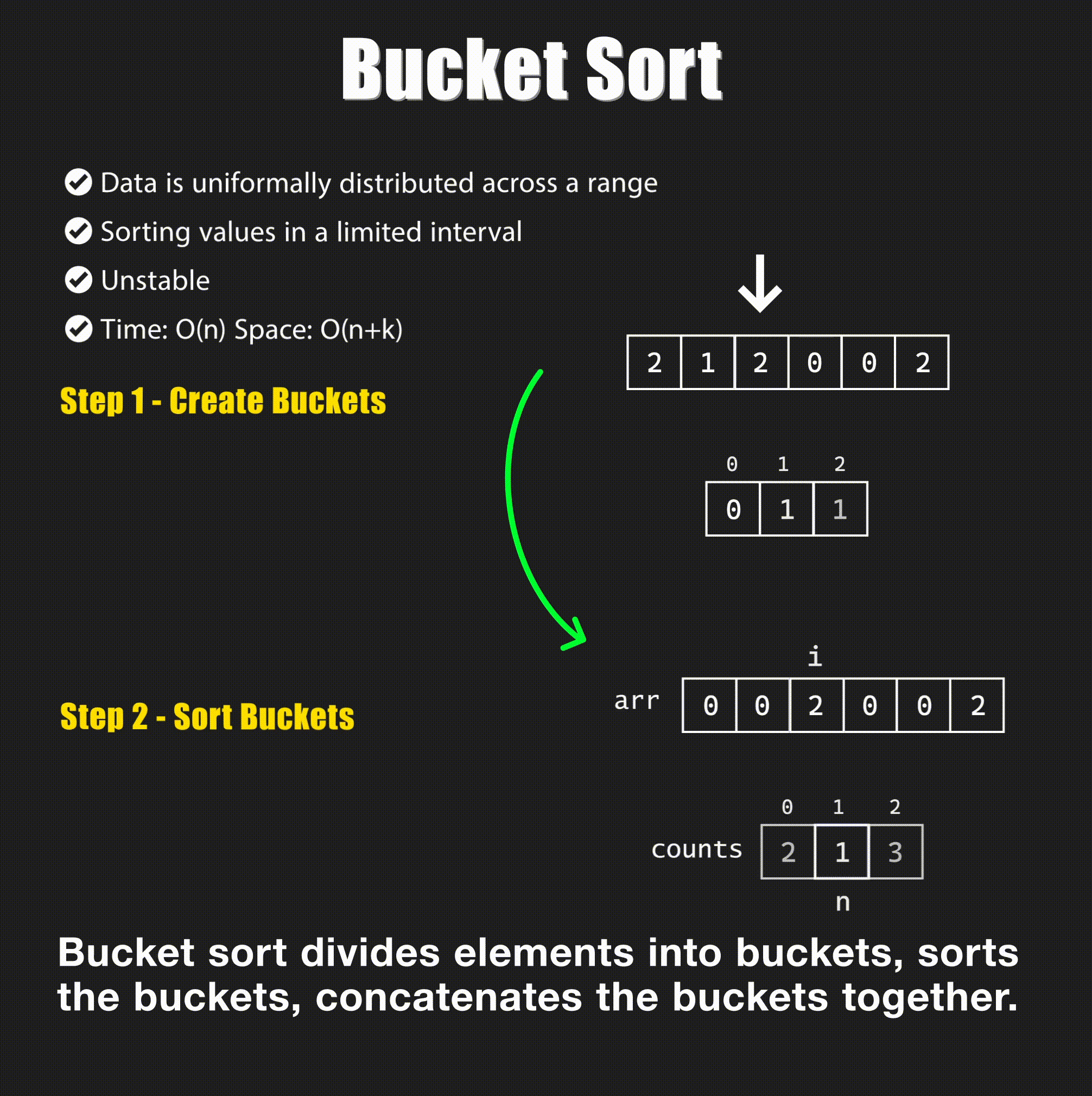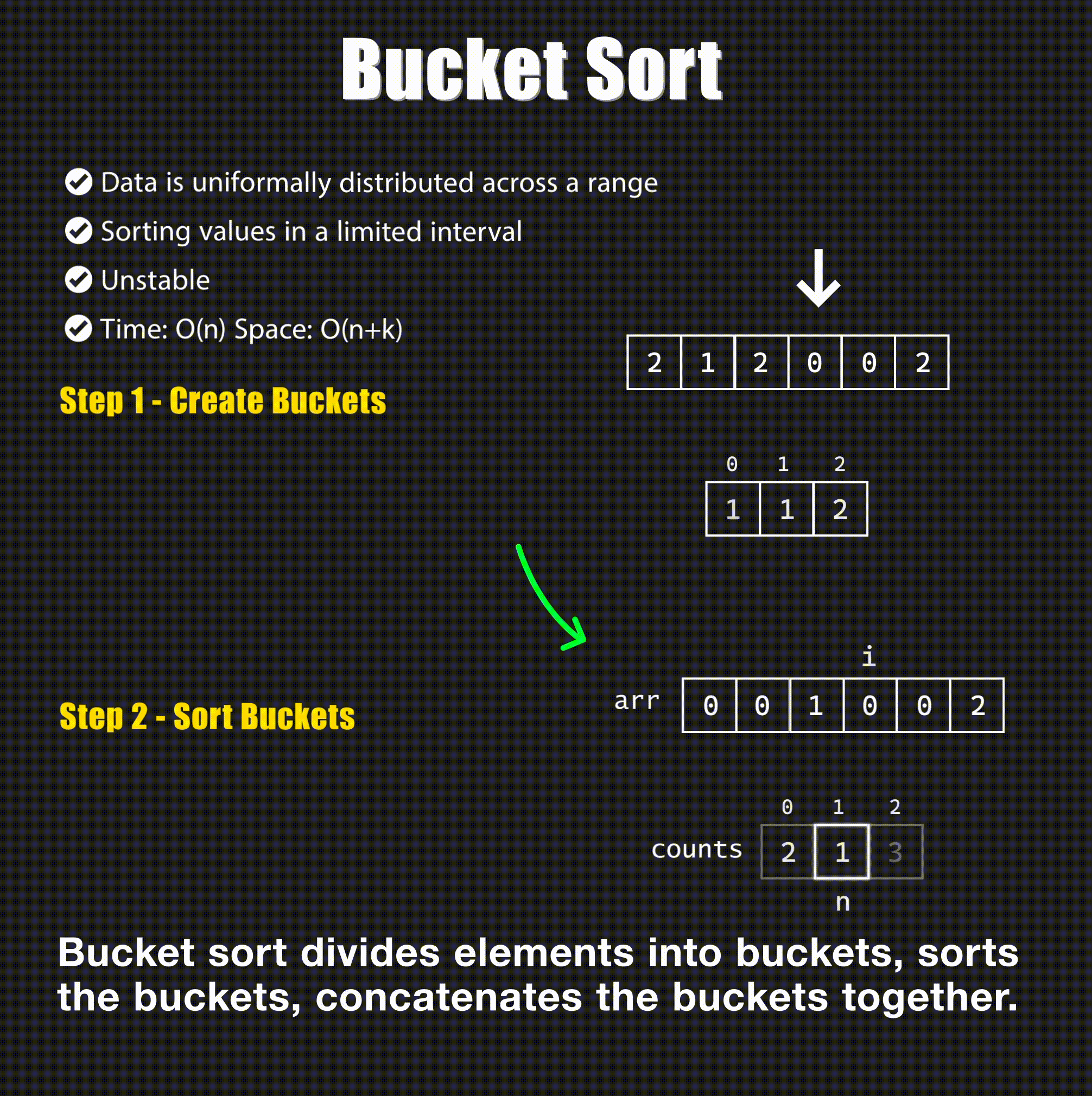
📊 4. Bucket Sort
Concept: Bucket Sort distributes elements into buckets and sorts each bucket individually.
Visual:
Python:
def bucket_sort(arr):
if not arr:
return arr
max_val, min_val = max(arr), min(arr)
bucket_range = (max_val - min_val) / len(arr)
buckets = [[] for _ in range(len(arr) + 1)]
for i in arr:
if i == max_val:
bucket_idx = len(arr) - 1
else:
bucket_idx = int((i - min_val) / bucket_range)
buckets[bucket_idx].append(i)
for bucket in buckets:
bucket.sort()
result = []
for bucket in buckets:
result.extend(bucket)
return result
Complexity:
Time: O(n)
Space: O(n + k)